
Echantillonage et dématriçage
Echantillonage/reconstitution d'un signal
Echantillonage d'un signal
L'échantillonage d'un signal est l'opération qui consiste à transformer un signal analogique en signal numérique.
Nous allons prendre comme premier exemple la transformation d'une onde sonore en signal numérique. Cette transformation est celle utilisée classiquement pour la création des CD audios.
Un signal sonore peut être vu comme la somme de fonctions sinusoidales (nous en avons discuté dans le chapitre consacré aux ondes planes). Nous allons donc nous consacrer à l'échantillonage d'un signal sinusoïdal (les résultats s'étendraient de toutes façons à toutes les formes de signaux périodiques en appliquant le théorème de décomposition en séries de Fourier).
L'échantillonage consiste à mesurer la valeur du signal de façon périodique, en espaçant les points de mesure d'une "distance" constante. Dans le cas d'un signal temporel (cas de l'onde sonore), les mesures seront faites à intervalle temporel constant. Nous voyons dans le schéma ci-dessous l'exemple d'un signal sinusoidal de fréquence 1Hz (une période par seconde) qui est échantilloné à une fréquence de 50Hz (50points par seconde).
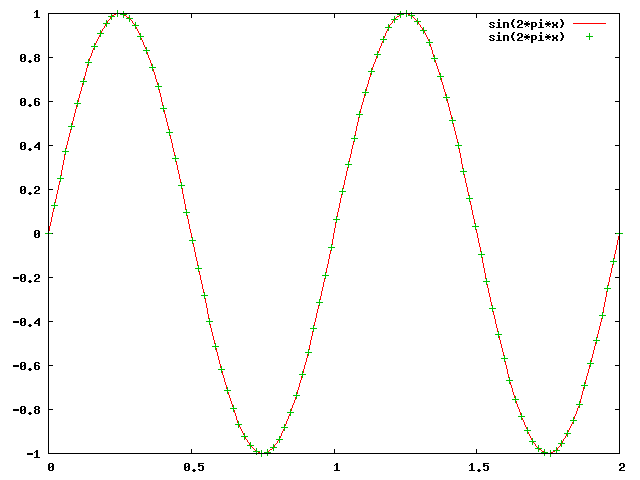
Le signal est en rouge, et les points verts représentents les points d'échantillonage. On transforme donc bien ainsi un signal analogique en une succession de valeurs numériques, qui correspond à l'ordonnée de chacun des points d'échantillonage (nous ne discuterons pas ici de la précision numérique utilisée pour chacun des points, ce problème est abordée en détail dans le chapitre consacré aux formats de fichiers et à la quantification des signaux).
Reconstitution d'un signal
Une fois le signal échantilloné, il peut être stocké sous forme numérique. Il faudra cependant le transformer à nouveau en signal analogique physique lors de son utilisation. On réalise alors une opération connue sous le nom d'interpolation, qui consiste à reconstruire la courbe qui relie les points d'échantillonage. Cette courbe sera de plus ou moins bonne qualité, suivant que le signal a été échantilloné plus ou moins finement. Ainsi, pour le signal précédent à 1Hz, échantilloné à 50Hz, la reconstruction est quasi-parfaite. En revanche, pour le signal ci-dessous, toujours à 1Hz mais échantilloné seulement à 5Hz, la courbe finale obtenue est loin de ressembler à une belle sinusoide.
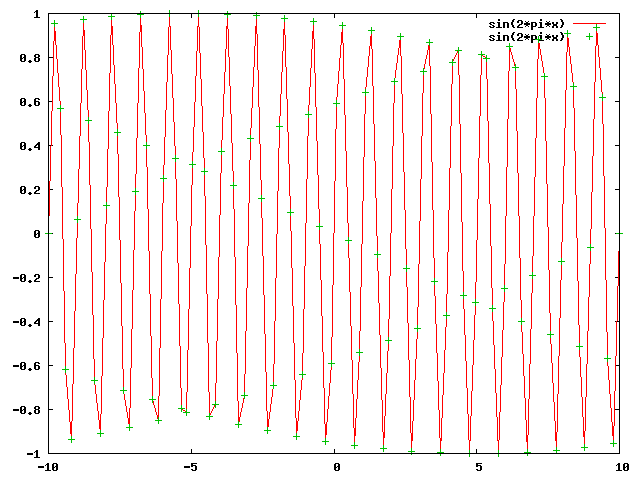
Il existe des techniques qui permettent d'améliorer la qualité de la courbe reconstitutée. La technique la plus utilisée est l'interpolation basée sur la fonction: $$ \mathrm{sinc}(x)=\frac{\sin(\pi x)}{\pi x} $$
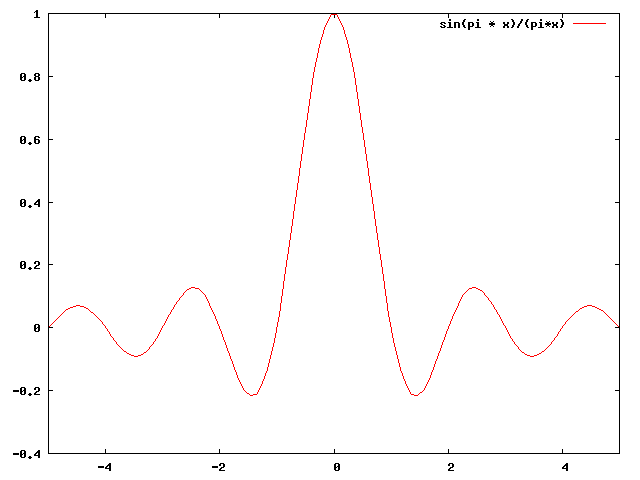
Chaque valeur résultant de l'échantillonage est multiplié par la fonction $\mathrm{sinc}(x)$, décalé de façon à ce que'elle ait son maximum à l'instant précis d'échantillonage considéré, et qu'elle vaille 0 pour tous les autres instants d'échantillonage. L'ensemble de ces fonctions est alors sommé pour reconstruire le signal final. Cette formule d'interpolation est connue sous le nom de formule de Whittaker-Shannon: $$ x(t)=\sum{x[n]\ \mathrm{sinc}\left(\frac{t-n T}{T}\right)} $$ Ici $ T = 1/f $, où $f$ est la fréquence d'échantillonage.
Cette formule n'est pas applicable en pratique car elle demande une sommation sur un trés grand nombre de termes. D'autres techniques sont utilisées, par exemple dans les convertisseurs digital/analogique des platines laser.
Cependant, avec une fréquence d'échantillonage trop petite par rapport à la fréquence du signal, une partie de l'information est perdue de façon irrémédiable.
Théorème de Nyquist-Shannon
La question que l'on est en droit de se poser est de savoir à partir de quelle fréquence d'échantillonage l'information contenue dans le signal d'origine est perdue de façon irrémédiable, au point que la reconstruction donnera un signal radicalement différent du signal originel.
C'est à cette question que répond le théorème de
Nyquist-Shannon.
Considérons un signal:
$$x(t)=\cos(2 \pi f t)$$
Si nous l'échantillonons avec une fréquence de 1/T, nous
obtiendrons la séquence de nombres suivante:
$$
x_n=\cos(2 \pi n f T)
$$
Si maintenant nous considérons le signal:
$$y(t)=\cos(2 \pi (1/T-f) t)$$
Si nous l'échantillonons à la même fréquence, nous
obtenons:
$$y_n=\cos(2 \pi n (1/T-f) T) = \cos(2 \pi n f T)$$
Les deux signaux sont donc différents, mais ont le même échantillonage. On voit ci-dessous un exemple (approximatif) d'un tel résultat; les échantillons (points noirs) ne permettent pas de distinguer le signal $\cos(x)$ et le signal $\cos(8x)$.
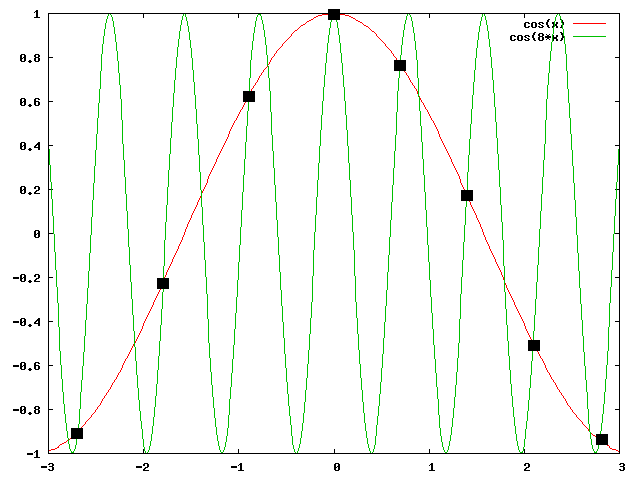
Pour distinguer l'échantillonage de deux signaux il faut que: $$(1/T-f) \gt f\ \mathrm{soit}\ 1/T > 2f $$
On voit donc que pour échantilloner correctement un signal, il faut employer une fréquence qui est supérieure ou égale au double de la fréquence du signal à échantilloner. Pour en revenir à notre exemple des CD de musique, nous savons que l'oreille humaine est sensible aux sons jusqu'à 20KhZ. L'industrie du disque a donc normalisé comme fréquence d'échantillonage 44Khz (44000 points par seconde), soit un peu plus que le double de 20Khz.
Application à la photographie
Le théorème de Nyquist-Shannon s'applique parfaitement dans le cas de la photographie numérique. Une image est en effet un signal analogique spatial (et non temporel), mais cela ne modifie en rien les conditions de Nyquist.
Appliqué à la photographie, et en supposant que nous utilisons des capteurs de type X3 Foveon (chaque photosite capte les trois couleurs), le théoréme de Nyquist nous indique qu'un capteur ne peut saisir des détails que si leur fréquence est la moitié de sa fréquence d'échantillonage.
Prenons un exemple (hypothétique) simple. Supposons que nos disposions d'un capteur Foveon disposant de 6 millions de photosite, soit une résolution de 3000x2000, et que nous photographions "plein cadre" une feuille de papier de 30x20cm. La taille minimale d'un détail "captable" sera de :
20/(2000/2)=20/1000=2/100=0.02cm=0.2mm
Il s'agit là bien entendu de la limite théorique du capteur, connu aussi sous le nom de fréquence d'extinction. Cette limite théorique est bien entendu affectée par l'ensemble des éléments optiques qui se trouvent entre l'objet et le capteur, et la limite réelle de résolution est toujours plus faible que la fréquence d'extinction...
Un autre problème, autrement plus sérieux, se pose dans la grande majorité des cas: la plupart des capteurs ne sont pas des Foveon X3 mais bien plutôt des capteurs basés sur la mosaïque Bayer. Avec de tels capteurs, la fréquence d'échantillonage du vert est le double de celle du rouge ou bleu, mais n'est que la moitié d'un capteur Foveon X3, et un pixel ne possède qu'une seule information de couleur. Il se pose donc le problème de tenter de reconstruire les informations manquantes. Cette opération est généralement appelée dématriçage ou démosaïquage.
Mosaïque Bayer et dématriçage
Introduction
La mosaïque Bayer est une alternance de capteurs Rouge, Vert et Bleu. Cette alternance de capteurs est réalisée en plaçant sur chaque photodiode un filtre de la couleur complémentaire. Par exemple, la photodiode qui doit recueillir l'information "Bleue" est recouverte d'une superposition de deux filtres: un cyan et un magenta.
Il faut savoir que Nikon a utilisé des matrices couleurs différentes, basées sur un système Cyan/Magenta/Jaune/Vert au lieu d'un système RVB (par exemple sur le Coolpix 900), avec une fréquence d'échantillonage identique pour les 4 couleurs (le capteur était, à ma connaissance, fabriqué par Sony). Cela présentait l'avantage de n'utiliser qu'un seul filtre au lieu de deux, pour trois couleurs (CMY) sur quatre, mais il semble que ce système soit aujourd'hui abandonné(le dernier Nikon à l'utiliser semble être le Coolpix 4300, en Aout 2002), et nous n'en parlerons plus dans la suite de ce chapitre.
Un capteur Bayer ressemble donc à ceci:

Les mosaïques Bayer peuvent être légèrement différentes suivant la façon dont les pixels R,V et B sont agencés, mais le principe général reste le même. il y a deux fois plus de capteurs verts que de capteurs rouges ou bleus. La fréquence d'échantillonage du vert est donc le double du rouge ou du bleu. Le vert est favorisé car l'oeil humain a son pic de sensibilité dans cette frange spectrale (voir notre chapitre sur la perception de la couleur).
Il faut maintenant reconstruire les informations manquantes. En effet, chaque pixel ne contient qu'une seule information de couleur, et il faut trouver le meilleur algorithme permettant de retrouver l'information manquante sur les deux autres couleurs. C'est le but du dématriçage ou demosaïquage.
Nous allons montrer sur un exemple à quoi ressemble un détail de photographie avant dematriçage. Nous allons détailler la photo suivante et plus particulièrement la boucle supérieure du B inscrite dans le rectangle:


Cela nous donne, en agrandissant de façon à rendre les pixels visibles, les deux images suivantes, avant et après dématriçage.


Nous allons maintenant nous intéresser aux différents algorithmes employés. Il en existe des dizaines, et la littérature est vaste au niveau de la recherche sur le sujet. De nombreux types de méthodes sont employés. Nous ne les détaillerons pas toutes! Le lecteur intéressé peut se pencher sur les nombreux articles disponibles en ligne (pour qui parle anglais, bien sûr). Un excellent article, sur lequel nous nous sommes appuyés, est celui de Gunturk qui fait un bilan plus détaillé mais plus technique, que le notre. Il est disponible ici.
Dématriçage bilinéaire ou bicubique
Les méthodes d'interpolation bilinéaire et bicubique sont des méthodes mathématiques classiques. Leur application au dématriçage ne fait appel qu'à une version très simple de ces méthodes. Regardons tout d'abord la matrice Bayer suivante:

Le but est de reconstruire la valeur verte du pixel 0, que nous noterons G0.
La méthode bilinéaire calcule la valeur de ce pixel suivant la formule: $$ G_0=\frac{G_1+G_2+G_3+G_4}{4} $$
La méthode bicubique utilisera les informations des pixels verts situés dans le cube de centre le pixel 0 et de rayon 2 (suivant la norme max). Nous aurons donc: $$ G_0=\alpha \frac{G_1+G_2+G_3+G_4}{4}+(1-\alpha) \frac{G_5+G_6+G_7+G_8+G_9+G_10+G_11+G_12}{8} $$ Pour $\alpha=1$ nous retrouvons la méthode bilinéaire. Le choix de $\alpha$ dépend de la façon dont on souhaite voir intervenir les pixels "extérieurs" dans le coloriage du pixel 0.
Le dématriçage bicubique est de mauvaise qualité. Il fait apparaitre des artefacts colorés désagréables rapidement; on peut voir ci-dessous, côte à côte, l'image telle qu'elle devrait être, et la façon dont l'algorithme bicubique la reconstruit:


Interpolation dirigée par l'orientation des bords
L'exemple précédent met clairement en évidence la faiblesse des méthodes bilinéaires ou bicubiques. Elles sont efficaces dans les régions régulières de l'espace, mais laissent apparaitre des artefacts dans les zones comportant des bords ou des bandes.
Une première idée consiste donc à rechercher une direction préférentielle suivant laquelle effectuer l'interpolation.

On va utiliser les informations de couleurs "certaines" qui sont, pour le point 0, les informations concernant le rouge. On calcule tout d'abord les gradients verticaux et horizontaux de variation du rouge: \begin{align*} \Delta H&=\left|\frac{R3+R6}{2}-R0\right|\\ \Delta V&=\left|\frac{R1+R8}{2}-R0\right| \end{align*} Trois cas peuvent se présenter: \begin{align*} \Delta V \gt \Delta H\ &\mathrm{alors}\ G_0=\frac{G_2+G_7}{2}\\ \Delta H \gt \Delta V\ &\mathrm{alors}\ G_0=\frac{G_4+G_5}{2}\\ \Delta H = \Delta V\ &\mathrm{alors}\ G_0=\frac{G_2+G_4+G_5+G_7}{4} \end{align*}
Cette méthode se base sur la prémisse que la variation d'intensité est corrélée entre tous les canaux lumineux.
Cette méthode peut être améliorée en utilisant des informations du second ordre lors du calcul des gradients. Ainsi, on peut calculer ΔH et ΔV de la façon suivante: \begin{align*} \Delta H&=\left|G_5-G_4\right|+\left|R_0-R_3+R_0-R_6\right|\\ \Delta V&=\left|G_7-G_2\right|+\left|R_0-R_1+R_0-R_8\right| \end{align*} On se retrouve alors face aux trois cas précédents: \begin{align*} \Delta V \gt \Delta H\ &\mathrm{alors}\ G_0=\frac{G_2+G_7}{2}+ \frac{R_0-R_1+R_0-R_8}{4}\\ \Delta H \gt \Delta V\ &\mathrm{alors}\ G_0=\frac{G_4+G_5}{2}+ \frac{R_0-R_3+R_0-R_6}{4}\\ \Delta H = \Delta V\ &\mathrm{alors}\ G_0=\frac{G_2+G_4+G_5+G_7}{4}+ \frac{R_0-R_3+R_0-R_6+R_0-R_1+R_0-R_8}{8} \end{align*}
Ce type de méthode peut-être adaptée de multiples façons en modififant les métriques utilisées.
Reconnaissance de formes
L'inconvénient des méthodes présentées ci-dessus est qu'elles ne recherchent une direction d'interpolation que dans le sens vertical ou horizontal. Il peut être intéressant de rechercher des gradients suivant d'autres directions afin de détecter les directions de plus fortes variations. Une extension relativement simple consiste à travailler suivant huit directions au lieu de quatre. Mais des solutions plus complexes peuvent être envisagées.
Méthode du vecteur médian
Cette méthode se base sur la construction d'un vecteur de pseudo-pixels en chaque point de l'image. Ce vecteur est construit en minimisant une fonction relativement simple qui ne dépend que de l'environnement 3x3 du point donné. Nous allons nous intéresser à la construction des composantes RVB du pseudo-pixel 5 de la mosaïque suivante.

On construit à partir de la sous matrice 3x3 (numérotée de 1 à 9) ci-dessus toutes les combinaisons possibles de couleurs concernant des pixels adjacents de cette sous matrice. Il y en a exactement 8: $(R_2,G_1,B_4), (R_2,G_3,B_6), (R_8,G_7,B_4), (R_8,G_9,B_6), (R2,G5,B4), (R_2,G_5,B_6), (R_8,G_5,B_4), (R_8,G_5,B_6)$. Nous noterons ces vecteurs: $(y_{ij})_{(i=1,3;j=1,8})$. Avec cette notation $y_{23}=G_7$.
Pour déterminer la valeur des pseudo-pixels RGB en 5, nous résolvons le problème de minimisation: $$ \argmin_{x_1,x_2,x_3} \sum_{j=1}^8 \sqrt{\sum_{i=1}^3 (x_i-y_{ij})^2} $$ Nous cherchons donc le point de coordonnée $(x1,x2,x3)$ qui soit le plus "au centre possible" de l'ensemble des autres points (il s'agit d'une minimisation de la somme des distances aux autres points). Il faut noter qu'une telle méthode va construire un point RGB dont la composante $G$ calculée n'est pas égale à la valeur réellement observée $G_5$.
Enfin, rappelons que ce problème de minimisation ne peut se traiter que de façon numérique et itérative, ce qui condamne cette méthode à une utilisation "hors ligne".
Réseaux de neurones
Le problème de reconstruction de l'information peut aussi être vu comme un problème de prédiction. On peut donc tenter d'utiliser des réseaux de neurones pour prédire les valeurs manquantes. Il s'agit là d'utiliser des réseaux de neurones supervisés, et donc de fournir une base d'apprentissage aux réseaux.
On peut utiliser des images issues d'une base de donnée, ou construire soi-même une base de données d'images en réduisant des photographies. Il suffit par exemple de transformer une image 3000x2001 issue d'une mosaique Bayer en image 1000x667 pour laquelle nous aurons une bonne fiabilité sur les couleurs. Cette image peut ensuite être "Bayérisé" en supprimant deux informations de couleurs sur trois suivant le schéma de la mosaïque Bayer, pour se retrouver avec une mosaïque Bayer 1000x667.
Ces images peuvent alors facilement être utilisées à la fois comme base d'apprentissage, et comme base de vérification.
Autres méthodes
Il existe encore bien d'autres méthodes. Parmi celles-ci on peut citer les approches bayesiennes (qui consistent à utiliser de l'information "à priori", comme la régularité spatiale ou la distribution du bruit, dans la recherche de la solution).
Une autre méthode travaille par reconstruction inverse, en modélisant la formation de l'image à partir des propriétés du senseur et du système optique.
Conclusion
Quelles que soient les méthodes utilisées, il faut bien se souvenir que le processus de dematriçage consiste à essayer de reconstruire une information qui est, de toutes façons, perdue. Lorsque l'on utilise un réseau de neurones sur une base d'apprentissage, l'idée sous-jacente est qu'il existe une fonction "boite noire", que le réseau parviendra à approximer. Dans le cas précédent, le problème est sous-déterminé. Il n'existe pas une, mais bien plusieurs fonctions, et l'on espère simplement que le modèle que l'on construit répond à une certaine forme de "logique" dans la formation d'images "de tous les jours".
Filtre anti-aliasing, ou passe-bas
Malgré l'efficacité des algorithmes présentés ci-dessus, la mosaïque Bayer diminue la fréquence d'échantillonnage par rapport à un capteur Foveon X3 de même densité. Si l'on est excessivement pessimiste, on peut aller jusqu'à dire que la fréquence d'échantillonage est réduite d'un facteur 3 sur le bleu et le rouge, et d'un facteur 2 sur le vert.
Comme on l'a vu précédemment, la disparité entre les fréquences d'échantillonnage à tendance à faire apparaitre des artefacts colorés de type moiré, très dérangeants pour l'oeil humain. Afin de réduire ce phénomène, les fabricants d'appreils numériques placent souvent devant le capteur de l'appareil un filtre anti-aliasing, ou filtre passe-bas, si l'on se réfère à la théorie fréquentielle. On voit sur la photographie suivante le système de capture de l'EOS-5D.

Le filtre passe-bas est placé à l'avant du capteur (et dans le cas du 5D, il porte également un quartz piezzo-électrique qui le fait vibrer au démarrage pour éliminer la poussière).
Un filtre passe-bas optique est constitué par une fine couche de cristal bi-réfringent (en général à base de beryl). Un cristal bi-réfringent est un cristal anisotrope (il n'est pas homogène dans l'espace). A ce titre, ce cristal a un indice de réfraction différent suivant la polarisation de la lumière qui le traverse. On observe alors une double réflexion dès que la lumière incidente n'est pas parallèle à l'axe optique du cristal (il existe quelques matériaux bi-axes, qui ont deux axes optiques au lieu d'un). Un des rayons suit une trajectoire dite ordinaire (qui correspond à une réfraction normale) suivant un indice notée $n_o$ et le second une trajectoire extraordinaire. Techniquement, l'indice de réfraction $n_e$ permettant de trouver le trajet du rayon extraordinaire se calcule à partir des composantes du vecteur d'excitation électrique $D(p,q,r)$ et de trois constantes $n_x,n_y,n_z$ qui ne dépendent que de la nature du cristal: $$ \frac{1}{n_e^2}=\frac{p^2}{n_x^2}+\frac{q^2}{n_y^2}+\frac{r^2}{n_z^2} $$ Pour mémoire le vecteur D se calcule en fonction du vecteur champ électrique E et de la polarisation P avec $$ D = \epsilon_0 E + P $$ L'écart $\Delta n=n_e-n_o$ est appelé bi-réfringence du milieu. Elle vaut en général quelques pourcents. Lorsque $\Delta n \gt 0$ on parle de bi-réfringence positive et lorsque $\Delta n \lt 0$ on parle de bi-réfringence négative.
Lorsque le cristal reçoit deux paquets de photons identiques au niveau de la direction du faisceau, mais ayant des polarisations différentes, il va les transformer en paquets de photons parallèles. Ainsi, pour une lumière naturelle non polarisée, qui présente des photons de toute polarisation, un même point va émettre des paquets de photons qui seront dispersés par le cristal bi-réfringent.
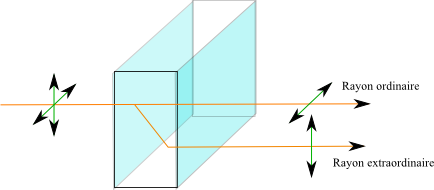
On peut voir ci-dessous l'effet d'un cristal de calcite bi-réfringent:

Pour la photographie, on utilise souvent du lithium-niobate
(LiNbO3), qui est un cristal biréfringent uniaxe
négatif. Les caractéristiques complètes du lithium-niobate sont
disponibles
ici. Le lithium-niobate n'est
transmissif qu'entre 400nm et 5000nm, ce qui en fait un
excellent candidat pour la transmission optique, et même un bon
filtre UV, mais pas un filtre IR. Comme pour la majorité des
matériaux, les coefficients de réfraction du lithium-niobate
dépendent de la longueur d'onde. Ils sont donnés par l'équation
de Sellmeier:
$$
n=\sqrt{A+\frac{B}{\lambda^2+C}+D\lambda^2}
$$
$\lambda$ est exprimé en micron (il varie donc
grossièrement entre 0.4 et 0.7 dans le spectre visible). Les
constantes $A$, $B$, $C$ et $D$ valent: $ A=4.9048,B=0.11768,
C=-0.0475,D=-0.027169$ pour le rayon ordinaire $A=4.582,
B=0.099169,C=-0.044432,D=-0.02195$ pour le rayon extraordinaire
On peut voir sur les figures suivantes la variation des
indices ordinaires et extraordinaires ainsi que la variation de
la réfringence en fonction de la longueur d'onde:
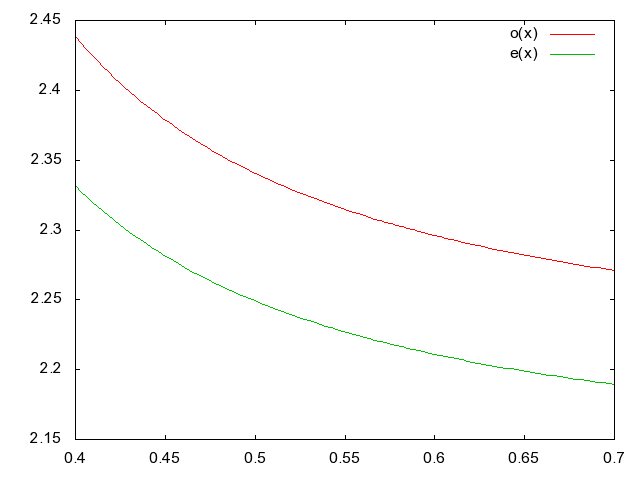
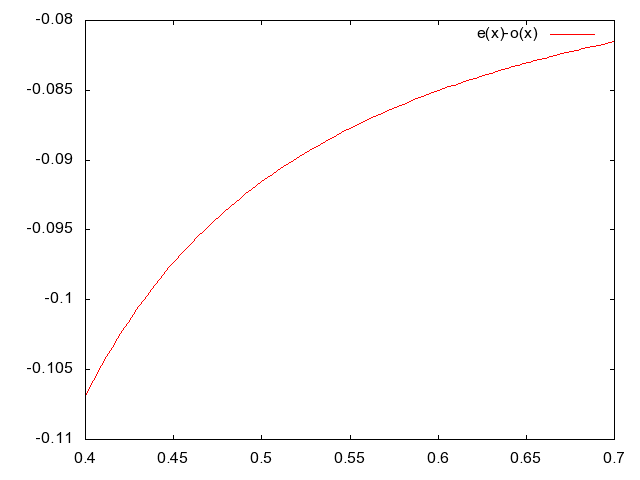
On calcule en général l'épaisseur du cristal pour qu'il diffuse les rayons issus d'un même point sur un diamètre de l'ordre de la surface de deux pixels. D'autre part, on place souvent deux couches de cristal l'une derrière l'autre, mais en décalant la seconde de 90 degrés par rapport à la première. Un même rayon sera alors réparti sur une surface couvrant une matrice de 2x2 capteurs.
Le filtre anti-aliasing a pour effet de diminuer les effets de moiré, mais il réduit aussi la finesse maximale de détail que l'on est capable d'atteindre. Le calcul exact de ces filtres est un secret commercial bien gardé.
Il faut également savoir que certains constructeurs renoncent volontairement au filtre anti-aliasing. Ainsi le Kodak DCS-14n n'a pas de filtre d'anti-aliasing, pas plus que le Leica M8 (qui a d'ailleurs un capteur KODAK, le KAF-10500). Certains dos moyen format numériques n'ont pas non plus de filtre passe-bas. Le débat sur le filtre passe-bas fait généralement rage dans la communauté des forums sur internet. On voit dans la photographie ci-dessous un exemple posté sur un de ces forums pour un dos moyen format Megavision S3 monté sur un Fuji GX-680 III.


A gauche, la photographie sortie "brut de capteur". Le moiré est visible nettement sur la feuille marron en haut à gauche, et fait apparaitre des taches colorées vertes et mauves. Il est le résultat de l'interaction entre la trame d'impression (il s'agit d'une étiquette) et la trame de capture (la matrice Bayer du capteur).
A droite, la même image après traitement par un filtre passe-bas numérique. Les artefacts colorés ont disparu.
Il est difficile de savoir quel choix est le bon. Renoncer au filtre passe-bas permet de capturer un peu plus de détail, mais fait jouer à la roulette russe concernant les effets de Moiré, qui pourront cependant être corrigés par des filtres numériques de post-traitement. Poser un filtre passe-bas optique fait disparaitre les effets de Moiré, mais réduit en partie la résolution maximale admissible. Dans certains cas, comme celui du Leica M8, le choix d'abandonner le filtre passe-bas était plutôt du à la volonté de réduire au maximum l'épaisseur de verre sur le capteur lui-même afin de renforcer l'efficacité du réseau de micro-lentilles (les appareils de type Leica ont des objectifs dont le design diffère de celui des objectifs des reflex; en raison de l'absence de miroir, les sorties des objectifs sont plus proches du capteur. Cela permet de construire des objectifs plus petits et plus légers que les objectifs rétro-focus, mais augmente la quantité de rayons tombant sur le capteur avec une forte incidence. Or les capteurs numériques sont peu efficaces sur les rayons à forte incidence, et nécessitent l'emploi de réseaux complexes de micro-lentilles posées sur le capteur, qui doivent reconcentrer la lumière.)
En fait, l'absence de filtre passe-bas se justifie dès
lors que les photographies seront faites en format RAW; dans ce
cadre, le post-traitement permettra de faire disparaitre les
effets de moiré. En revanche, si les photographies sont faites
en JPEG, la perte d'information liée à ce format est susceptible
de limiter l'efficacité des filtres numériques de
post-traitement.
Les dos moyen-format dans leur majorité
n'utilisent pas de filtre passe-bas, car les professionnels qui
les emploient utilisent presque exclusivement le format RAW. Il
est certain que sur des appareils bas de gamme destinés au grand
public, les filtre passe-bas sont indispensables. Entre les
deux, le débat a un sens. Pentax, avec le K10D, a été un des premiers à se distinguer
quelque peu en utilisant un filtre passe-bas qui est anisotrope.
D'autres comme Canon proposent sur le très haut de gamme (5Ds
par exemple) la possibilité de choisir entre appareil équipé
d'un filtre passe bas (5Ds) et appareil sans filtre passe-bas
(5DsR).
Il faut cependant savoir qu'il n'est pas tout a fait équivalent d'appliquer un filtre passe-bas optique ou un filtre passe-bas numérique en post-processing sur des appareils équipés de mosaïque Bayer. Nous allons le montrer dans le paragraphe suivant.
Comprendre les filtres bi-réfringents en terme de théorie fréquentielle
On parle en permanence de filtre passe-bas pour les filtres bi-réfringents. Cela vient simplement du fait qu'ils éliminent les composantes de plus haute fréquence spatiale. En fonction de la différence de réfringence, les rayons sont plus ou moins dispersées et vont donc "brouiller" l'image (la rendre plus floue), et ce de façon d'autant plus importante que la bi-réfringence est forte.
En théorie fréquentielle, un filtre $H$ s'appliquant à un signal $S_{in}$ peut toujours s'écrire sous la forme d'une convolution. Il existe deux formes permettant d'exprimer une convolution, suivant que le signal est continu (forme intégrale) ou qu'il est discrétisé (sommation). Nous allons nous intéresser à la simple sommation: $$ S_{out}(n)=S_{in} * H = \sum_m S(n-m)H(m) $$
Cela signifie que le signal de sortie au point $n$ est égal à la somme, avec $m$ variant sur la totalité des points de l'image, du signal au point $(n-m)$ multiplié par la valeur du filtre au point $m$. Notons également que ce formalisme est également employé dans le cadre de la description des anomalies optiques engendrées par un appareil quelconque (télescope, objectif, etc...) En effet, dans ce cas, les erreurs de coma, d'astigmatisme, etc peuvent être ramenées à un filtre appelé généralement Point Spreading Function (PSF) dont l'action est très similaire à celle d'un filtre passe-bas...
Cela peut paraitre bien compliqué, alors que c'est finalement extrèmement simple, et nous allons le voir sur un exemple. Considérons une simple fente laissant passer un signal lumineux monochromatique. Si ce signal a été discrétisé, nous pouvons représenter sa valeur en tout point de la fente par la valeur de son intensité, que nous noterons sous la forme du vecteur $S_{in}$. Un filtre bi-réfringent "parfait" tel que nous l'avons décrit plus haut n'est alors rien d'autre qu'une fonction telle que $H(0)=H(1)=0.5$ et telle que $H(m)=0$ pour $m$ différent de 0 et de 1. Donc, l'application de ce filtre se ramène à une simple multiplication matricielle du vecteur du signal d'entrée par une matrice dont la diagonale et la ligne située au dessus de la diagonale valent 0.5. Le filtre agit finalement comme une sorte de "moyenne glissante" qui fait une moyenne entre le signal du point courant et celui de son voisin immédiat.
La question qu'il est donc alors raisonnable de se poser est de savoir s'il est possible de retrouver le signal d'origine, dans la mesure où nous connaissons la forme exacte du filtre. La réponse est évidemment oui dans ce cas (qui est particulèrement simple): l'opération de déconvolution consiste simplement à inverser la matrice du filtre H ce qui dans le cas présent ne pose aucun problème (l'inverse se calcule analytiquement sans aucune difficulté).
Malheureusement (ou heureusement, car sinon les filtre passe-bas
optiques n'auraient aucun intérêt...) les choses ne sont pas
aussi simples avec les mosaiques Bayer. En effet, dans la
"vraie" vie, le signal optique n'est pas monochromatique, et il
est décrit non pas par une simple intensité en chaque point mais
bien par sa distribution de puissance $D(f,n)$
ou $f$ varie sur les fréquences du spectre visible.
Certes, nous pouvons toujours décrire notre filtre
bi-réfringent comme une matrice s'appliquant sur les
distributions spectrales en tout point, et le signal de sortie
vaudra par exemple:
$$D_{out}(f,n)=\frac{D(f,n)+D(f,n-1)}{2}$$
De façon générale, nous aurons toujours: $$ D_{out}(f,n)=D_{in}(f,n)*H=\sum_m D_{in}(n-m,f) H(m) $$ Mais la matrice Bayer va ensuite appliquer en chaque point du signal de sortie une seconde opération qui va transformer cette distribution spectrale en une intensité scalaire : $$ S(n)=\int D_{out}(f,n) P_n(f) df $$
Ici, $P_n(f)$ est une fonction de pondération qui dépend du site de la mosaique que touche le rayon lumineux. Elle vaudra $R(f)$, $G(f)$ ou $B(f)$. Ces courbes ont les formes suivantes:
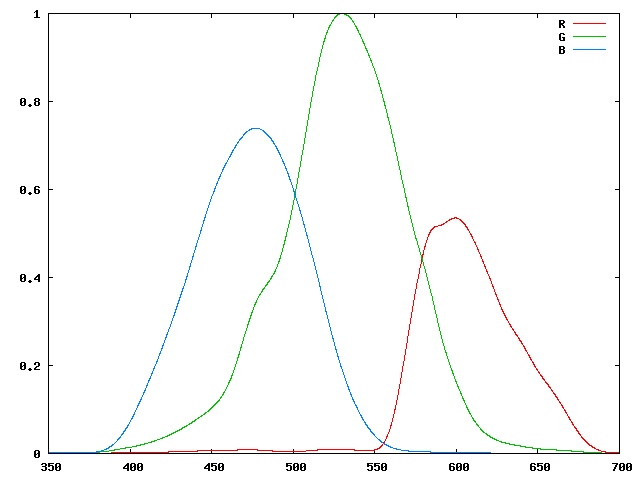
En développant l'expression ci-dessus, nous obtenons: $$ S(n)=\int \sum_m D_{in}(n-m,f) H(m) P_n(f) df $$ Si maintenant nous supposons que nous n'employons aucun filtre passe-bas optique avant notre mosaique Bayer, le signal de sortie original sera: $$ S_0(n)=\int D_{in}(n,f) P_n(f) df $$ Si nous employons maintnant un filtre passe bas numérique, la sortie réelle va maintenant: $$ S'(n)=S_0*H=\sum_m S_0(n-m)H(m)=\sum_m\left(\int D_{in}(n-m,f)P_{n-m}(f) df \right) H(m) $$ Ou encore: $$ S'(n)=\int \sum_m D_{in}(n-m,f) H(m) P_{n-m}(f) df $$ Nous constatons donc que $S(n)$ et $S'(n)$ ne sont pas égaux car $P_n$ n'est pas égal à $P_{n-m}$. Un filtre passe-bas numérique appliqué lors du post-processing n'aura pas le même effet qu'un filtre passe-bas optique appliqué avant la mosaïque Bayer.
Ressources en ligne
- Signal processing magazine, Janvier 2005
- IEEE transaction on signal processing, Mars 2005 Janvier 2005
- Electronic Imaging, Janvier 2004
- 30 ans de demosaiçage l'excellent papier (2005) de David Aleysson
Le téléchargement ou la reproduction des documents et photographies
présents sur ce site sont autorisés à condition que leur origine soit
explicitement mentionnée et que leur utilisation
se limite à des fins non commerciales, notamment de recherche,
d'éducation et d'enseignement.
Tous droits réservés.
Dernière modification: 09:08, 21/03/2024